Principio
de Pascal
Es una ley
enunciada por el físico y matemático francés Blaise Pascal entre1623–1662 estipula que la presión ejercida sobre
un fluido poco compresible y
en equilibrio dentro de un recipiente de paredes indeformables se transmite con
igual intensidad en todas las direcciones y en todos los puntos del fluido.
Una
parte muy fundamental sobre este principio es la prensa hidráulica es una
máquina compleja que permite amplificar las fuerzas y constituye el fundamento
de elevadores, prensas hidráulicas, frenos y muchos otros dispositivos
hidráulicos.
La
misma constituye la aplicación fundamental del principio de Pascal y también un
dispositivo que permite entender mejor su significado. Consiste, en esencia, en
dos cilindros de diferente sección comunicados entre sí, y cuyo interior está
completamente lleno de un líquido que puede ser agua o aceite.
Dos émbolos de
secciones diferentes se ajustan, respectivamente, en cada uno de los dos
cilindros, de modo que estén en contacto con el líquido. . Cuando sobre el émbolo de menor sección A1 se
ejerce una fuerza F1 la presión p1 que
se origina en el líquido en contacto con él se transmite íntegramente y de
forma casi instantánea a todo el resto del líquido. Por el principio de Pascal
esta presión será igual a la presión p2 que
ejerce el fluido en la sección A2, es decir:
Presión
La presión es la magnitud escalar que relaciona la fuerza con la
superficie sobre la cual actúa, es decir, equivale a la fuerza que actúa sobre
la superficie.
Cuando sobre una superficie plana
de área A se aplica una fuerza normal F de
manera uniforme, la presión P viene dada de la siguiente
forma:
En un caso general donde la fuerza puede tener cualquier dirección y no
estar distribuida uniformemente en cada punto la presión se define como:
Donde n es un vector unitario y normal a la superficie
en el punto donde se pretende medir la presión. La definición anterior puede
escribirse también como:
Donde:
, es la fuerza por unidad de superficie.
, es el vector normal a la superficie.
, es el área total de la superficie S.
Presión absoluta y relativa
En determinadas aplicaciones la presión se mide no como la presión
absoluta sino como la presión por encima de la presión atmosférica, denominándose presión relativa, presión normal, presión de gauge o presión manométrica.
Consecuentemente, la presión absoluta es la presión atmosférica (Pa)
más la presión manométrica (Pm) (presión que se mide con el
manómetro).
Presión hidrostática e hidrodinámica
En un fluido en movimiento la presión hidrostática puede diferir
de la llamada presión hidrodinámica por lo que debe especificarse a cuál de las
dos se está refiriendo una cierta medida de presión.
Presión de un gas
En el marco de la teoría cinética la presión de un gas es explicada como
el resultado macroscópico de las fuerzas implicadas por las colisiones de las
moléculas del gas con las paredes del contenedor. La presión puede definirse
por lo tanto haciendo referencia a las propiedades microscópicas del gas:
Para un gas ideal con N moléculas, cada una de
masa m y moviéndose con una velocidad aleatoria promedio vrms contenido
en un volumen cúbico V las partículas del gas impactan con las
paredes del recipiente de una manera que puede calcularse de manera estadística
intercambiando momento lineal con las paredes en cada choque y efectuando una
fuerza neta por unidad de área que es la presión ejercida por el gas sobre la
superficie sólida.
La presión puede calcularse entonces como fórmula para un gas ideal
Este resultado es interesante y significativo no sólo por ofrecer una
forma de calcular la presión de un gas sino porque relaciona una variable
macroscópica observable, la presión, con la energía cinética promedio por
molécula, 1/2 mvrms², que es una magnitud microscópica
no observable directamente. Nótese que el producto de la presión por el volumen
del recipiente es dos tercios de la energía cinética total de las moléculas de
gas contenidas.
Propiedades de la presión en
un medio fluido
1.
La fuerza asociada a la presión en un
fluido ordinario en reposo se dirige siempre hacia el exterior del fluido, por
lo que debido al principio de acción y reacción, resulta en una compresión para
el fluido, jamás una tracción.
2.
La superficie libre de un líquido en
reposo (y situado en un campo gravitatorio constante) es siempre horizontal.
Eso es cierto sólo en la superficie de la Tierra y a simple vista, debido a la
acción de la gravedad constante. Si no hay acciones gravitatorias, la
superficie de un fluido es esférica y, por tanto, no horizontal.
3.
En los fluidos en reposo, un punto
cualquiera de una masa líquida está sometida a una presión que es función
únicamente de la profundidad a la que se encuentra el punto. Otro punto a la
misma profundidad, tendrá la misma presión. A la superficie imaginaria que pasa
por ambos puntos se llama superficie equipotencial de presión o superficie isobárica
El principio de Arquímedes
El principio de Arquímedes afirma que todo cuerpo sumergido en un fluido
experimenta un empuje vertical y hacia arriba igual al peso de fluido
desalojado.
La explicación del principio de Arquímedes consta de dos partes como se
indica en las figuras:
- El estudio de las fuerzas sobre una porción de
fluido en equilibrio con el resto del fluido.
- La sustitución de dicha porción de fluido por
un cuerpo sólido de la misma forma y dimensiones.
Ampliamos el principio de Arquímedes, a un cuerpo sumergido en un fluido en rotación

Consideremos, en primer lugar, las fuerzas sobre una porción de fluido
en equilibrio con el resto de fluido. La fuerza que ejerce la presión del
fluido sobre la superficie de separación es igual a p·dS,
donde p solamente depende de la profundidad y dS es
un elemento de superficie.
Puesto que la porción de fluido se
encuentra en equilibrio, la resultante de las fuerzas debidas
a la presión se debe anular con el peso de dicha porción de fluido. A esta resultante
la denominamos empuje y su punto de aplicación es el centro de masa de la
porción de fluido, denominado centro de empuje.
De este modo, para una porción de fluido en equilibrio con el resto, se
cumple
Empuje=peso=ρf·gV
El peso de la porción de fluido es igual al producto de la densidad del
fluido ρf por la aceleración de la gravedad g y
por el volumen de dicha porción V.
Se sustituye la porción de fluido por un cuerpo
sólido de la misma forma y dimensiones.
Si sustituimos la porción de fluido por un cuerpo sólido de la misma
forma y dimensiones. Las fuerzas debidas a la presión no cambian, por tanto, su
resultante que hemos denominado empuje es la misma y actúa en el mismo punto,
denominado centro de empuje. Lo que cambia es el peso del cuerpo sólido y su
punto de aplicación que es el centro de masa, que puede o no coincidir con el
centro de empuje. Por tanto, sobre el cuerpo actúan dos fuerzas: el empuje y el
peso del cuerpo, que no tienen en principio el mismo valor ni están aplicadas
en el mismo punto. En los casos más simples, supondremos que el sólido y el
fluido son homogéneos y por tanto, coincide el centro de masa del cuerpo con el
centro de empuje.
Flotación
entre dos líquidos no miscibles
Un cuerpo sólido está sumergido en dos líquidos inmiscibles: agua y
aceite. Determinaremos la densidad de dicho cuerpo por dos métodos distintos:
- El principio de Arquímedes
- La ecuación fundamental de la
estática de fluidos
El aceite que tiene una densidad 0.8 g/cm3 se sitúa en
la parte superior y el agua que es más densa 1.0 g/cm3 se sitúa
en la parte inferior del recipiente.
La densidad del bloque es un número comprendido entre la densidad del
aceite 0.8, y la del agua 1.0. Un cuerpo de esta densidad flota entre los dos
líquidos.
Conociendo que parte del sólido está sumergido en aceite (fluido 1) o en
agua (fluido 2), se determinará la densidad de dicho cuerpo.
El principio de Arquímedes nos dice que si el bloque está en equilibrio,
el peso del bloque debe ser igual al empuje proporcionado por ambos líquidos.
Peso del bloque =empuje del agua + empuje del aceite
ΡShg=ρ2Sxg+ρ1S(h-x)g
x=ρ−ρ1ρ2−ρ1hx=ρ−ρ1ρ2−ρ1h
S es
el área de la base del bloque, h su altura, y x es
la parte del bloque sumergida en agua.
En general, un cuerpo que flota en la superficie del agua, está
sumergido en dos fluidos, uno es el agua ρ2=1000 kg/m3 y
el otro es el aire ρ1=1.29 kg/m3.
Habitualmente, se desprecia la densidad del aire frente a la del sólido ρ y
la del fluido ρ2, aplicándose la fórmula aproximada
x≈ρρ2h
Ecuación fundamental
de la estática de fluidos
Sean p1 y p2 las
presiones sobre la cara superior e inferior del bloque sumergido.
La cara superior está en el aceite a una profundidad y.
La presión p1 será igual a la atmosférica p0 más la correspondiente a la altura y de
aceite.
p1=p0+ρ1gy
La cara inferior está en el agua. La presión p2 será igual a la presión atmosférica p0 más la correspondiente a la altura de aceite (y+h-x)
más la correspondiente a la altura de la columna de agua (x)
p2=p0+ρ1g(y+h-x)+ρ2gx
La fuerza que ejerce el fluido sobre dichas caras será el producto de la
presión por el área de su superficie S.
Como vemos en la figura, para que haya equilibrio se tiene que cumplir
que
p1S+mg=p2S
Teniendo en cuenta que m=ρ·hS despejamos
el valor de x.
x=ρ−ρ1ρ2−ρ1hx=ρ−ρ1ρ2−ρ1h
Es el mismo resultado que hemos obtenido aplicando el principio de
Arquímedes
El principio
de Arquímedes en un fluido en rotación
·
En un
fluido de densidad ρf en equilibrio, la presión crece
linealmente con la profundidad h, p=p0+ρfgh. p0 es la presión en la superficie del fluido
·
Un cuerpo
sumergido experimenta una fuerza de empuje hacia arriba, E=ρfgV
·
La fuerza
total sobre el cuerpo sumergido es el empuje E menos el
peso mg, F=(ρf−ρ)VgF=(ρf−ρ)Vg
Por otra parte,
·
En un
fluido en rotación con velocidad angular constante ω, la
presión crece proporcionalmente al cuadrado de la distancia al eje de
rotación, p(r)=12ρfω2r2p(r)=12ρfω2r2
·
Un cuerpo
sumergido experimenta una fuerza de empuje en la dirección radial, hacia el eje
de rotación E=ρf(ω2r0)V.
·
La fuerza
total sobre el cuerpo sumergido es la fuerza centrífuga menos el
empuje en la dirección radial, F=(ρ−ρf)Vω2r0F=(ρ−ρf)Vω2r0
En este apartado, vamos a calcular la fuerza de empuje que experimenta
una esfera de radio Rsumergida en un fluido de densidad ρf en rotación con velocidad angular constante ω,
el centro de la esfera está a una distancia r0=h del eje de rotación paralelo al eje Y
Vamos a seguir los mismos pasos que en el ejemplo de una esfera
sumergida en un fluido en equilibrio
El principio de Arquímedes se aplica a objetos de cualquier densidad. En caso de conocer la densidad del objeto, su comportamiento al estar sumergido dentro de un fluido puede ser:
1) Si el objeto es más denso que el fluido en el cual está sumergido, el objeto se hundirá.
2) Si la densidad del objeto es igual a la del fluido en el cual está sumergido, el objeto no se hundirá ni flotara.
3) Si el objeto es menos denso que el fluido en el cual está sumergido, el objeto flotara en la superficie del fluido.
Debido al efecto del empuje, los cuerpos sumergidos en un fluido tienen un peso aparentemente menor a su verdadero peso, y le llamamos peso aparente. El valor de la fuerza de empuje se determina mediante la diferencia del peso real y la del peso aparente, es decir:
Empuje = peso real – peso aparente
Como todo cuerpo que sea sumergido en un líquido se ajustara a una profundidad a la cual su peso sea igual al del agua desplazada, el peso del cuerpo está dado por la expresión:
Fcpo = Pcpo = ρcpo • Vcpo • g
y el peso del fluido desplazado o fuerza de empuje ejercida por el líquido está dada por la expresión:
E = ρliq • Vcpo • g
en donde:
E = es el empuje
Vcpo = el volumen que desplaza el cuerpo
ρliq = la densidad del líquido donde se sumerge el cuerpo
g = 9.81 m/s2
Como el peso específico (Pe) de la sustancia está dado por:
Pe = ρliq • g
Entonces también podemos escribir la expresión:
E = Pe • Vcpo
El producto del volumen del cuerpo por la densidad del fluido es igual a la masa del fluido desalojado, correspondiente a un volumen idéntico al que tiene el cuerpo sumergido. El producto de dicha masa por la aceleración de la gravedad nos da su peso. Por lo tanto. También podemos calcular el empuje que sufren los cuerpos que están sumergidos en un fluido usando la expresión:
E = Vcpo • ρliq•g = mlíq • g
De acuerdo a todo lo anterior, el empuje que recibe un cuerpo sumergido en un líquido puede determinarse por alguna de las siguientes expresiones:
Empuje = Peso del fluido desalojado
Empuje = Peso real – peso aparente en el líquido
Empuje = (densidad del cuerpo) (volumen del cuerpo sumergido) (gravedad)
E = ρcpo • Vcpo • g
Empuje = (Peso específico de la sustancia) (Volumen del líquido desalojado)
E = Pe • Vcpo
Empuje = (masa del líquido desplazado) (gravedad)
E = mlíq • g
Empuje = (densidad del líquido) (volumen del líquido desalojado) (gravedad)
E = ρliq • Vliq • g
Conviene recordar que para la aplicación de las fórmulas anteriores, en caso de que el cuerpo este totalmente sumergido, el volumen del cuerpo es igual al volumen de líquido desalojado, y que cuando el cuerpo flota parcialmente en el líquido, el volumen del líquido desalojado es igual solamente al volumen de la parte del cuerpo que se encuentra sumergido.
El concepto de empuje nos puede ayudar a determinar la densidad de un cuerpo sólido (ρcpo). Para ello determinamos primero la masa real mr del cuerpo con ayuda de una balanza. Después, sumergimos el objeto en un líquido de densidad conocida (ρliq.c), por ejemplo, el agua y determinamos la masa aparente del objeto ma, , la cual será menor que la anterior. De acuerdo al principio de Arquímedes, esta diferencia se debe al empuje del agua, y por lo tanto la diferencia mr - ma es igual a la masa del agua desalojada por el cuerpo. La densidad del cuerpo está dada por la expresión:
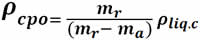
También podemos determinar la densidad de un líquido. Para ello, primero obtenemos la masa aparente ma de un cuerpo de masa mr sumergido en un líquido de densidad conocida (ρliq.c). La diferencia de masa (mr - ma) es igual a la masa del volumen de líquido desalojado, por lo tanto:
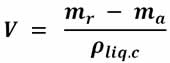
Después se introduce el mismo cuerpo en el líquido problema y hallamos su masa aparente ma2. De nuevo la diferencia de masa mr - ma2 es igual a la masa del volumen de líquido desalojado, por tanto:
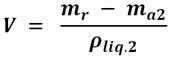
Puesto que el volumen debe ser igual en ambas ecuaciones, ya que el cuerpo es el mismo, tenemos que la densidad del líquido problema (desconocido) es:
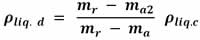
Algunas de las aplicaciones del principio de Arquímides son: la flotación de los barcos, la flotación de los submarinos, los salvavidas, los densímetros, los globos aerostáticos, los flotadores de las cajas de los inodoros, los peces.
Los barcos flotan porque su parte sumergida desaloja un volumen de agua cuyo peso es mayor que el peso del barco. Los materiales con los que está construido un barco son más densos que el agua. Pero como el barco está hueco por dentro, contiene una gran cantidad de aire. Debido a ello la densidad promedio del barco es menor que la del agua.
Debido a que, para que un objeto flote, la fuerza de flotación sobre el cuerpo debe ser igual al peso del fluido desplazado, los fluidos más densos ejercen una fuerza de empuje más grande que los menos densos. Por lo anterior, un barco flota más alto en agua salada que en agua dulce porque la primera es ligeramente menos densa.
Un submarino normalmente flota. Para un submarino es más fácil variar su peso que su volumen para lograr la densidad deseada. Para ello se deja entrar o salir agua de los tanques de lastre. De manera semejante, un cocodrilo aumenta su densidad promedio cuando traga piedras. Debido al aumento de su densidad (por las piedras tragadas), el cocodrilo puede sumergirse más bajo el agua y se expone menos a su presa.
Para que una persona flote en el agua con más facilidad, debe reducir su densidad. Para efectuar lo anterior la persona se coloca un chaleco salvavidas, provocando con ello aumentar su volumen mientras que su peso aumenta muy poco, por lo cual, su densidad se reduce.
Un pez normalmente tiene la misma densidad que el agua y puede regularla al extender o comprimir el volumen de una bolsa con la que cuenta. Los peces pueden moverse hacia arriba al aumentar su volumen (lo que disminuye su densidad) y para bajar lo reducen (lo que aumenta su densidad).
El densímetro o areómetro consiste en un tubo de vidrio con un tubo lleno de plomo para que flote verticalmente. La parte superior tiene una graduación que indica directamente la densidad del líquido en donde está colocado. Se utiliza para medir la cantidad de alcohol de un vino, para controlar la pureza de la leche, para saber si un acumulador está cargado (la carga depende de la concentración de ácido del líquido del acumulador).
TABLA 1 DENSIDAD DE DIFERENTES SUSTANCIAS
| Sustancia | Densidad (kg/m3) | Sustancia | Densidad (kg/m3) |
| Agua a 4 ºC | 1000 | Gasolina (20 ºC) | 700 |
| Agua (20 ºC) | 998 | Glicerina a 0ºC | 1250 |
| Agua de mar | 1030 | Hielo | 920 |
| Aire (0 ºC) | 1.30 | Helio | 0.18 |
| Aire (20 ºC) | 1.20 | Mercurio(0 ºC) | 13600 |
| Alcohol etílico | 790 | Oxigeno | 1.43 |
| Aluminio a 0ºC | 2700 | Oro a 0ºC | 19300 |
| Cobre a 0ºC | 8900 | Plata a 0ºC | 10500 |
| Corcho a 0ºC | 240 | Plomo | 11400 |
Ahora llevaremos a cabo la solución de algunos problemas aplicando el principio de Arquímides.
Ejemplo 1
Una esfera de cierto material es sumergida en agua, su masa aparente resultó ser de 91.3 g. Su masa real (en el aire) es de 100 g.
a) ¿Cuál es la densidad de dicha esfera?
b) Después sumergimos la misma esfera en otro líquido de densidad desconocida ρliq.d, y se encuentra que la masa aparente de la esfera es de 93.04 g. ¿Cuál es la densidad de este líquido?
Datos:
mr = 100 g = 0.100 kg
ma = 91.3 g = 0.0913 kg
ρagua = 1000 kg/m3
ρliq.d = 1000 kg/m3
a )Fórmula:
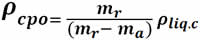
Sustitución y resultado:
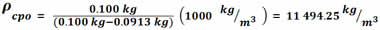
De acuerdo a la tabla de densidades, deducimos que la esfera es de plomo, cuya densidad es de 11400 kg/m3
b) Datos:
mr = 100 g = 0.100 kg
ma = 91.3 g = 0.0913 kg
ρagua = 1000 kg/m3
ma2 = 93.04 g = 0.09304 kg
Fórmula:
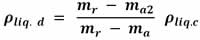
Sustitución:
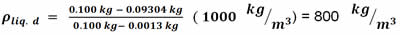
Teorema de Bernoulli
Es una aplicación directa del
principio de conservación de energía. Con otras palabras está diciendo que si
el fluido no intercambia energía con el exterior (por medio de motores,
rozamiento, térmica...) esta ha de permanecer constante.
El teorema considera los tres únicos
tipos de energía que posee el fluido que pueden cambiar de un punto a otro de
la conducción. Estos tipos son; energía cinética, energía potencial
gravitatoria y la energía debida a la presión de flujo (hidrostática). Veamos
cada una de ellas por separado:
Por lo tanto el teorema de Bernoulli se expresa de
la siguiente forma:
Donde:
·
v es la velocidad de flujo del fluido en la
sección considerada.
·
g es la constante de gravedad.
·
h es la altura desde una cota de referencia.
·
p es la presión a lo largo de la línea de
corriente del fluido (p minúscula).
·
ρ es la densidad del fluido.
Si consideramos dos puntos de la misma conducción
(1 y 2) la ecuación queda:
Donde m es constante por ser un sistema cerrado y V
también lo es por ser un fluido incompresible. Dividiendo todos los términos
por V, se obtiene la forma más común de la ecuación de Bernoulli, en función de
la densidad del fluido:
Una simplifación que en muchos casos es aceptable es considerar el caso en que la altura es constante, entonces la expresión de la ecuación de Bernoulli, se convierte en:





















